Ein Taschenrechner - delphi-lernen.de

Oder auch: Hallo-Welt - mit Zahlen

Hierbei wollen wir den Umgang mit Variablen in einem praktischen Beispiel durchführen. Dabei kümmern wir uns erst um die "ganzen" Zahlen und dann in die reellen bzw. Fließkomma-Zahlen.

Teil 1: Ein Taschenrechner für ganze Zahlen

Hier nun eine "Mitmach"-Anleitung:

Wir starten ein neues Projekt: Windows-VCL-Anwendung.
Gleich zu Beginn, speichern wir alles in einem Ordner (z.B. Taschenrechner1): Projektname: "Taschenrechner1", Unit-Name: "MainUnit".
Wir ziehen 12 Edit-Felder (3*4 für die vier Rechenarten) in das Formular und reihen es entsprechend 4 Zeilen und 3 Spalten an.
Im Objektinspektor löschen wir bei allen Edit-Feldern die Eigenschaft "Text".
Zudem benennen wir die Edit-Felder um: im Objektinspektor unter "Name" immer das Kürzel "Ed" mit der mit ihm verbundenen Funktion: Beispiele: EdSummand1, EdSummand2, EdSumme, EdMinuend, EdFaktor1, EdDividend, ...
Nun brauchen wir noch 4 Labels: jeweils zwischen die ersten Zusammengehörenden Edit-Felder und schreiben als "Caption" das zugehörige Rechenzeichen.
Wenn die Labels plaziert sind, verfahren wir genauso wie bei Schritt 4 mit dem Kürzel "Lbl" (Beispiel: lblPlus...)
Dann brauchen wir im Zwischenraum zwischen der Rechnung und dem Ergebnis-Feld jeweils ein Button mit dem Caption "=" und dem Namen zusammengesetzt aus "Btn"+Rechenoperator (Bsp: "BtnSumme").

Nun sollte das Formular in etwa so aussehen:

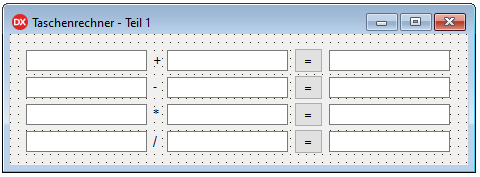
Okee, bei Form1 habe ich den Titel geändert ;)

Die grafische Arbeit ist nun erledigt. Lasst uns nun programmieren:
Per Doppelklick (in der Design-Ansicht) auf BtnSumme gelangen wir zur automatisch erstellten BtnSummeClick-Prozedur, welche ausgeführt wird, wenn wir später auf den Button einmal klicken.
Nun in der Code-Ansicht deklarieren wir zunächst zwei Variablen, die uns als Speicherplätze für Ganzzahlen dienen sollen. Hierzu fügen wir zwischen der "procedure"-Zeile und dem "begin" folgendes ein:

procedure TForm1.BtnSummeClick(Sender: TObject);
var
a, b, c : Integer;
begin

Tastenkürzel F11

Mit der F11 kann zwischen Code-Ansicht, Formular-Ansicht und dem Objektinspektor gewechselt werden. Eine kleine Taste ist meistens schneller im Einsatz, als mit der Maus auf ein Element zu "zielen" und zu klicken.

Tastenkürzel F12

Falls wir keine Eigenschaft ändern wollen, geht mit F12 der Wechsel zwischen Code-Ansicht und Formular-Ansicht auch direkt.

Alles, was zwischen "begin" und "end;" steht, ist der Code, der ausgeführt wird. Hier Initialisieren wir zunächst die Variablen a und b, indem wir ihnen die in EdSummand1 und EdSummand2 eingegebenen Werte zuweisen. Das ":=" ist in Delphi eine Wert-Zuweisung. Da EdSummand1 eine Instanz des Objektes TEdit ist, müssen wir auf eine Eigenschaft zugreifen um den Wert nutzen zu können.

Hinweis: Dies ist nun der Erste Schritt in OOP:

Das "Objekt" TEdit hat die Eigenschaft "Text" vom Typ TCaption (Was im Grunde ein String ist).
Schreibend sowie auch lesend können wir nun wie folgt darauf zugreifen:

	
begin

  // schreibend:

  EdSummand1.Text:='Dies ist ein Text';

  // lesend (z.b. bei Anzeige einer Meldung soll der Eingegebene Text gezeigt werden):

  ShowMessage(EdSummand1.Text);

end;

Ok, Ausflug beendet - nun wollen wir den Summand1 und Summand2 auslesen und die Summe in EdSumme schreiben. Dabei haben wir aber noch eine Hürde: Den String in eine Zahl umwandeln.
Lösung: Wir konvertieren den String in einen Integer-Wert mit der Funktion "StrToInt" ;-)

	
begin

  a := StrToInt( EdSummand1.Text);  

  // ...

end;

und das gleiche mit dem zweiten Summanden in einer neuen Zeile.

Nun lassen wir ihn mal rechnen, indem wir in einer weiteren neuen Zeile c die Summe aus a und b zuweisen:

c := a+b;
Die Summe, die in der Variablen c steht, möchten wir nun in das Feld EdSumme schreiben:

EdSumme.Text := IntToStr( c);
Mit einem Klick auf das grüne "Wiedergabe"-Symbol in der Symbolleiste oder F9 können wir testen, ob die Addition funktioniert.

Wir wiederholen die Schritte von 6 bis 13 entsprechend für die Subtraktion und die Multiplikation.
Die Division ist etwas schwerer, weshalb wir da jetzt nochmal etwas genauer darauf eingehen:

Wie manche es vielleicht von Excel kennen, kann man sich vorstellen, dass der Divisions-Operator ein Slash (/) ist. Dies gilt allerdings nicht für Ganzzahlen (wie bereits bei Step 04 "Rechenoperatoren" angesprochen). Da haben wir ja das Problem, dass bei einer Division ein "Rest" existieren kann. Die Operatoren für diese Rechnung lauten DIV und MOD.

DIV gibt den ganzzahligen Wert der Division zurück (Bsp: 17 DIV 3 ergibt 5).

MOD gibt den Rest zurück (Bsp: 17 MOD 3 ergibt 2).

Im Vergleich mit den Anderen Rechenoperationen, brauchen wir hier somit eine zusätzliche Variable "d" für den Rest der Division. Wir wiederholen also auch die Schritte 6 bis 13.
Bei Schritt 12 wird c entsprechend a DIV b zugewiesen und die neue Variable d bekommt a MOD b als Ergebnis.
Bei Schritt 13 nutzen wir die String-Addition um die Ausgabe etwas "schön" darstellen zu können.
StrToInt(c) + ' Rest ' + StrToInt(d);

Alles abspeichern, starten, testen und fertig ;-)

Da bei der Division möglicherweise Probleme entstehen können, hier nochmal die ganze Prozedur:

	
procedure TForm1.BtnDivisionClick( Sender: TObject);

var

  a, b, c, d : Integer;

begin

  a := StrToInt( EdDivident.Text);

  b := StrToInt( EdDivisor.Text);

  c := a div b;

  d := a mod b;

  EdQuotient.Text := IntToStr( c) + ' Rest ' + IntToStr( d);

end;

Unter GitHub befindet sich der komplette Sourcecode des Taschenrechners als Musterlösung.

Teil 2: Ein Taschenrechner für reelle Zahlen

Um den Part abzukürzen: Hier sind Schritte 1-8 identisch.
Man kann auch das Projekt aus a komplett in einen neuen Ordner kopieren, alle unnötigen Dateien löschen (alles bis auf .dpr, .dproj, .pas, .dfm), die .dproj öffnen, die entsprechenden Programmteile abändern.

Hier kurz die allgemeinen Unterschiede:

Als Variablentyp nehmen wir statt "Integer" -> "Double";
Die Funktion "StrToInt" tauschen wir mit "StrToFloat" aus;
Umgekehrt benötigen wir auch für die Umwandlung der Gleitkommazahl in einen String eine andere Funktion wie "IntToStr", die Lösung: "IntToFloat";
Mit Datei -> "Projekt speichern unter" können wir das Projekt unter "Taschenrechner2" abspeichern.

Diese allgemeinen Unterschiede sind für Addition, Subtraktion und Multiplikation schnell umgesetzt. Die Division war für die Ganzzahlen etwas präziser, so dass wir sowohl die korrekte Ganzzahl-Division und auch den Rest der Division korrekt anzeigen lassen zu können. Die Division hat nun aber keinen Rest mehr und wir können somit auch bei der Division die Berechnung genauso aufbauen, wie bei den drei anderen Grundrechenarten. Als Divisions-Zeichen gilt "/".

Alles abspeichern, starten, testen und fertig ;-)

Auch für diesen zweiten Teil ist unter GitHub der komplette Sourcecode als Musterlösung.

Hier ein Überblick zu den wichtigsten Operatoren.

(a,b,c,i sind vom Typ Integer, mit b ungleich 0;
d, e, r vom Typ Real;
s, s1..s5 vom Typ String mit Inhalt: s1:='abc', s2:='def'....)

Operator

Bedeutung

Beispiele

+,-,*

Zahlenarithmetik
Anwendung bei Ganz- sowie Kommazahlen

	
i := a+b;

c := (i-1)*a+(b-1);

d := e*(a+r)*(a-r);

DIV, MOD

Division von Ganzzahlen

	
i := a div b;

i := 91000 div 1000 mod 60; // = 31

i := 91000 mod 60 div 1000; // = 0

Division von Kommazahlen

	
r := a/b; 

r := (a+c)/(d+e)

// Achtung: folgende Zeile ist inkorrekt:

i := a/b;

Zusammenführen von Strings

	
s1 := 'hallo';

s2 := 'welt';

leerzeichen := ' '; 

s3 := s1+leerzeichen+s2; // = 'hallo welt'

s := '';                  // leerer String.

s4 := s2+s3+s2;          // 'weltwelt'

Die Funktionen Inc() und Dec():

Wenn du eine Ganzzahl (also Integer) nur um eins (1) erhöhen willst, dann kann die Methode Inc() dafür genutzt werden. Um eins runterzuzählen verwendet man Dec():

	
var

    zahl : Integer;

begin

    zahl := 1;

    Inc(zahl);

    // zahl ist nun 2

    Dec(zahl);

    Edit1.text = IntToStr(zahl); // in Edit1 steht nun "1"

end;

Und nun noch einmal der Hinweis: Der Sourcecode liegt unter GitHub als Musterlösung.
Viel Spaß ;)